The Combinatorial Nature of Modern AI

Back in mid-2022 my Twitter feed was filled with debates about whether deep learning would stall without neuro-symbolic hybrids. Gary Marcus, for instance, laid out the case plainly in Deep Learning Is Hitting a Wall and has continued to press it in later posts and interviews^{1 2}. Symbols matter, no doubt. Yet the last few years suggest that plain neural methods are already doing a surprising amount of symbolic work internally.

Two paradigms

In the past decade, there has been a lot of progress on solving combinatorial optimization problems using neural networks. While there are many classic problems to tackle, like the Traveling Salesman Problem (TSP), Maximum Independent Set, and Max-Cut, the literature has converged on two broad approaches.

Reinforcement learning

A first camp learns policies to perform actions that move within the set of feasible solutions. A canonical example is the work by Kool et al.³, which trained what is almost exactly a standard Transformer model to construct TSP tours one node at a time with REINFORCE and a greedy-rollout baseline, achieving near-optimal solutions for up to 100-node graphs. Crucially, the policy is entirely learned without hand-crafted heuristics. Parallel work learns improvement policies that iteratively refine initial tours using local edits like 2-opt⁴.

Why does RL naturally fit here? TSP is fundamentally a problem over permutations and, while it can be encoded as a quadratic unconstrained binary optimization (QUBO) problem using one-hot vectors, the binary formulation creates a large, unwieldy search space for learning⁵. A sequential policy that directly produces permutations avoids the detour through $\{0,1\}$ variables and can operate on a relatively small action space. RL remains sample-hungry, though, with Kool’s model training on millions of TSP instances.

Why an attention-based model and not an RNN? In Transformer models, KV-caches behave like banks of symbols that attention reads on demand, while the MLPs can be viewed as persistent key-value stores. This division of labor makes optimization easier than routing everything through one recurrent state. As shown in recent work, attention retrieves and MLPs memorize, which is a strong inductive bias for discrete decision-making⁶. Put simply, the architecture allows manipulation of symbols on demand.

As a concrete example, consider how heuristics for TSP perform node selection based on criteria like distance to the partial tour or regret (the additional cost of delaying a node). These heuristics are easy to encode as message-passing steps with max-aggregation over scalars, so a naive ’neural’ approach could simply repeat message-passing over a high-dimensional hidden state (this is the Structure2Vec model). Larger latent dimensions accelerate convergence during training, but the model still cannot process symbolic information because aggregation is element-wise. Attention, by contrast, performs a (soft) max-aggregation over vectors, which unlocks symbolic processing.

Unsupervised methods

A second camp minimizes an energy, often directly over QUBOs. Diffusion-based solvers cast discrete problems into a denoising process over $\{0,1\}^n$ and learn schedules that steer samples toward high-quality solutions⁷. Recent work explores discrete diffusion specifically for unsupervised combinatorial optimization^{8 9}. Another line smooths objective functions via heat diffusion while provably preserving optima, then optimizes the smoothed versions to guide search more effectively¹⁰.

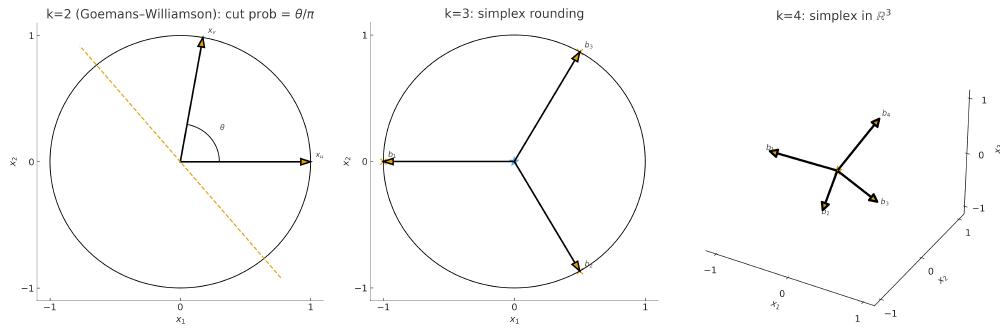
There is also a non-probabilistic path that relaxes the QUBO into a semidefinite program (SDP). Yau et al. show that a graph neural network (OptGNN) can represent optimal approximation algorithms for a broad class of constraint-satisfaction problems. Their model performs a gradient update on an SDP objective at each layer, then projects the embeddings back to a discrete space via an inner product with a random direction¹¹. This mirrors classic relaxation techniques. For example, the Goemans–Williamson algorithm solves Max-Cut by relaxing binary variables to unit vectors, optimizing an SDP, then rounding with a random hyperplane. Extensions to the Max-$k$-Cut place vectors on a simplex with $k$ equidistant directions before rounding¹² (see diagram below). OptGNN effectively subsumes the Goemans–Williamson approximation for Max-Cut into a learned pipeline and supports the intuition that a message-passing neural network can learn a schedule of gradient-like steps on a quadratic objective.

Connection to modern AI models

Much of the success of machine learning in combinatorial optimization is complementary to recent research on interpretability of LLMs. A helpful mental model is that each token in an LLM is a symbol and each layer maps it to a new one in a high-dimensional dictionary. Anthropic’s interpretability program gives concrete evidence that such dictionaries exist and can be sparsified into human-named features with sparse autoencoders. See Toy Models of Superposition and the large-scale follow-up Scaling Monosemanticity^{13 14}. If deep nets operate on vector relaxations that get projected back to discrete decisions, it is no surprise that they often behave like symbol processors.

Given that Transformers excel at combinatorial optimization due to the attention mechanism and classic approximation algorithms can be ’neuralized’, we ask: what other principles in combinatorial optimization are transferable to neural architectures? Here are a few ideas:

Baker’s technique. Baker’s PTAS covers many problems on planar graphs by layering the graph, solving bounded-treewidth subproblems, then stitching the results to get a $1+\epsilon$ approximation in polynomial time for fixed $\epsilon$. Neural variants now mimic this decomposition. NN-Baker learns to produce Baker-style layerings and dynamic-programming decisions and shows strong performance for Maximum Independent Set and related problems¹⁵.

Geometry-aware attention. The famous PTAS for Euclidean TSP is due to Arora (and independently Mitchell). For any $\epsilon>0$, it returns a $(1+\epsilon)$-approximation in polynomial time for fixed dimension using randomized quad-trees and dynamic programming¹⁶. Recent architectures have started building metric structure into attention. The Erwin transformer organizes points with ball-tree partitions and computes localized attention that scales nearly linearly while capturing global context through hierarchical coarsening and cross-ball interactions¹⁷.

Energy inside the model. Another direction is to keep autograd in the loop and let the network learn energy landscapes and schedules. Energy-Based Transformers make decoding itself an optimization that is trained end-to-end¹⁸.

Summary

Evidence shows that classic approximation algorithms naturally integrate into neural architectures, and LLMs seem to work on vector relaxations that are converted back to discrete symbols. This indicates that the symbolic reasoning capabilities advocated by Gary Marcus might already be developing within purely neural systems. Although not explicit symbolic manipulation, these learned representations are effectively capturing the essential combinatorial structure through approximation.